Diskreetne Fourier' teisendus

Diskreetne Fourier' teisendus (lühend DFT inglise keele sõnadest discrete Fourier transform) on pideva Fourier' teisenduse vaste digiteeritud (ajas diskreeditud ja nivoos kvanditud) funktsioonide ja signaalide jaoks. Teatud tingimustel on DFT tulemused vastavuses pideva Fourier' teisenduse tulemustega. Kuid paljudel juhtudel on tulemused siiski oluliselt erinevad, mistõttu DFT tulemuste ülekandmisel analoogsignaalidele tuleb olla ettevaatlik.

Fourier' teisenduse ja diskreetse Fourier' teisenduse vaheline suhe. Vasak veerg: Pidev funktsioon (ülemine) ja tema Fourier' teisendus (all). Kesk-vasak veerg: Originaalfunktsiooni perioodiline summeerimine (ülemine). Fourier' teisendus (alumine) on null, v.a diskreetsete punktide kohtadel. Pöördteisendus on sinusoidide summa – Fourier' rida. Kesk-parem veerg: Originaalfunktsioon on diskreeditud (ülemine). Selle Fourier' teisendus (alumine) on originaalteisenduse perioodiline summa. Parem veerg: DFT (alumine) arvutab diskreetseid proove pidevast diskreetse aja Fourier' teisendusest. Pöörd-DFT (ülemine) on originaalproovide perioodiline summeerimine. Kiire DFT arvutab ühe tsükli DFT-d ja pöörd-DFT-d ühes pöörd-DFT tsüklis.

Fourier' teisenduse kujutis (ülemine) ja selle perioodiline summa (DTFT) (alumine)

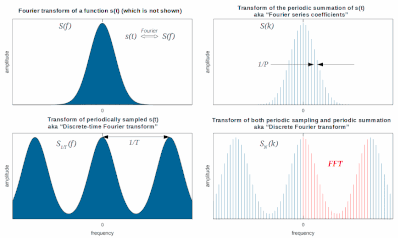
DFT on kõige olulisem diskreetne teisendus, mida kasutatakse Fourier' analüüsi teostamiseks paljudes praktilistes rakendustes. Signaalitöötluses on iga signaal funktsioon, millest võetakse proove (lugemeid signaali väärtustest) diskreetimissagedustel. Analüüsi objektideks võivad olla näiteks helilaine, raadiosignaal või muutuvad temperatuurinäidud. Pilditöötluses võivad proovid olla pikslite väärtused rasterkujutise igas reas või veerus. DFT-d kasutatakse ka selleks, et lahendada efektiivselt diferentsiaalvõrrandeid ja teha teisi toiminguid, nagu konvolutsioon ja suurte arvude korrutamine.

Kuna DFT tegeleb piiratud andmemahtudega, saab seda rakendada, arvutades numbriliste algoritmide abil või kasutades sihtotstarbelist riistvara. Need rakendused kasutavad tavaliselt Fourier' kiirteisendust ehk kiiret Fourier' teisendust (Fast Fourier Transform, FFT), mis põhineb teisendamiseks vajalike arvutuste mahu vähendamisel teatud (korduvate) tulemuste (korduva) ärakasutamise teel või mõne spetsiifilise vaheteisenduse kasutamise teel.

Mõiste

N kompleksarvude jada $x_{0},x_{1},\ldots ,x_{N-1}$ teisendatakse N-perioodiliseks kompleksarvude jadaks:

$X_{k}\ {\stackrel {\text{def}}{=}}\ \sum _{n=0}^{N-1}x_{n}\cdot e^{-2\pi ikn/N},\quad k\in \mathbb {Z} \,$ (täisarvud)  

Perioodilisuse tõttu on tegelikult arvutatud domeen k [0, N – 1]. See on alati nii, kui DFT-d on rakendatud kiire Fourier' teisenduse kaudu. Muud domeenid on [-A / 2, N / 2-1] (N paaris) ja [- (N – 1) / 2, (N – 1) / 2] (N paaritu), kui vasak ja parem pool DFT väljundis on vahetatud.

Diskreetne Fourier' teisendus on tavaliselt tähistatud tähega ${\mathcal {F}}$, kus $\mathbf {X} ={\mathcal {F}}\left\{\mathbf {x} \right\}$ või ${\mathcal {F}}\left(\mathbf {x} \right)$ või ${\mathcal {F}}\mathbf {x}$.

Definitsioonivõrrandit võib tõlgendada või tuletada mitmel viisil, näiteks:

• See kirjeldab täielikult diskreetse aja Fourier' N-perioodilist järjestust, mis sisaldab ainult diskreetse sageduse komponente.
• Samuti tagab see ühtlaste vahekaugusega proove sisalduva pideva DFT antud piiratud pikkusega.
• See on sisendandmete ristkorrelatsioon, $X_{n}$ ja kompleksne sinusoid sagedusel k/N. Seega see toimib nagu sobitatud filter sellele sagedusele.
• See on diskreetne analoog Fourier' rea koefitsientide leidmise valemile:

$x_{n}={\frac {1}{N}}\sum _{k=0}^{N-1}X_{k}\cdot e^{2\pi ikn/N},\quad n\in \mathbb {Z} \,$

mis on ka N-perioodiline. $\scriptstyle n\ \in \ [0,\ N-1]$ domeenis on see definitsiooni valemi pöördteisendus. Selle tõlgenduse järgi on iga $X_{k}$ kompleksne number, mis kodeerib funktsiooni $x_{n}$ komplekssesse siinuselisse komponenti  $(e^{2\pi ikn/N})$ nii amplituudi kui ka faasi. Siinuse sagedus on k/N. Amplituud ja faas vastavad võrranditele:

$|X_{k}|/N={\sqrt {\operatorname {Re} (X_{k})^{2}+\operatorname {Im} (X_{k})^{2}}}/N$

$\arg(X_{k})=\operatorname {atan2} {\big (}\operatorname {Im} (X_{k}),\operatorname {Re} (X_{k}){\big )}=-i\operatorname {ln} \left({\frac {X_{k}}{|X_{k}|}}\right),$

kus atan2 on arkustangensi funktsioon kahe argumendi jaoks.

Euleri valemi abil saab DFT valemi teisendada trigonomeetriliseks vormiks, mida kasutatakse inseneride arvutlustes ja infotehnoloogias:

Fourier teisendus: $X_{k}=\sum _{n=0}^{N-1}x_{n}\cdot (\cos(-2\pi k{\frac {n}{N}})+i\sin(-2\pi k{\frac {n}{N}})),\quad k\in \mathbb {Z} \,$

Pöördteisendus: $x_{n}={\frac {1}{N}}\sum _{k=0}^{N-1}X_{k}\cdot (\cos(2\pi k{\frac {n}{N}})+i\sin(2\pi k{\frac {n}{N}})),\quad n\in \mathbb {Z} \,$

kus

$N$ on proovide arv

$n$ on hetkel töödeldava proovi number (0, ..., $N-1$)

$x_{n}$ on signaali väärtus hetkel $n$

$k$ on sagedus (0 Hz kuni $N-1$ Hz) töötlemise hetkel

$X_{k}$ on sagedusega $k$ signaali (amplituudi ja faasi väljendav kompleksarv.

Omadused

Täielikkus

Diskreetne Fourier' teisendus on pööratav lineaarne teisendus

${\mathcal {F}}\colon \mathbb {C} ^{N}\to \mathbb {C} ^{N}$

kus $\mathbb {C}$ on kompleksarvude hulk. See tähendab, et iga N > 0, N-mõõtmeline kompleksvektor omab DFT-d ja PDFT-d (pöördteisendust), mis on omakorda N-mõõtmelised kompleksvektorid.

Ortogonaalsus

Vektorid $u_{k}=\left[e^{{\frac {2\pi i}{N}}kn}\;|\;n=0,1,\ldots ,N-1\right]^{T}$ moodustavad ortogonaalse baasi üle N-mõõtmeliste kompleksvektorite hulga:

$u_{k}^{T}u_{k'}^{*}=\sum _{n=0}^{N-1}\left(e^{{\frac {2\pi i}{N}}kn}\right)\left(e^{{\frac {2\pi i}{N}}(-k')n}\right)=\sum _{n=0}^{N-1}e^{{\frac {2\pi i}{N}}(k-k')n}=N~\delta _{kk'}$

kus$~\delta _{kk'}$ on Kronecker delta. (Viimane samm on triviaalsete $k=k'$ summa, kus 1+1+⋅⋅⋅=N, ja selline geomeetriline jada, millest saab summeerides saada kokku nulli.) Seda ortogonaalsuse tingimust saab kasutada selleks, et tuletada pöördteisenduse valemit DFT definitsioonist.

Planchereli teoreem ja Parsevali teoreem

Kui X_k ja Y_k on vastavalt x_n ja y_n teisendused, siis ütleb Parsevali teoreem, et:

$\sum _{n=0}^{N-1}x_{n}y_{n}^{*}={\frac {1}{N}}\sum _{k=0}^{N-1}X_{k}Y_{k}^{*}$

kus tärn tähendab kompleksset konjugatsiooni. Parsevali teoreemi selline erijuht, kus x_n = y_n, on Planchereli teoreem, mis väidab:

$\sum _{n=0}^{N-1}|x_{n}|^{2}={\frac {1}{N}}\sum _{k=0}^{N-1}|X_{k}|^{2}.$

Perioodilisus

Perioodilisust võib näha otse definitsioonist:

$X_{k+N}\ {\stackrel {\mathrm {def} }{=}}\ \sum _{n=0}^{N-1}x_{n}e^{-{\frac {2\pi i}{N}}(k+N)n}=\sum _{n=0}^{N-1}x_{n}e^{-{\frac {2\pi i}{N}}kn}\underbrace {e^{-2\pi in}} _{1}=\sum _{n=0}^{N-1}x_{n}e^{-{\frac {2\pi i}{N}}kn}=X_{k}.$

Samas on näha, et pöördteisenduse võrrand viib perioodilisele laiendamisele.

Nihe

Korrutades $x_{n}$ lineaarse faasiga $e^{{\frac {2\pi i}{N}}nm}$ mingi täisarvu m järgi vastab nihkele väljundis $X_{k}$: $X_{k}$, mis asendatakse $X_{k-m}$, kus indeks on tõlgendatud kui absoluutväärtus N (perioodiliselt). Samamoodi nihe sisendis $x_{n}$ vastab väljundi $X_{k}$ korrutamisele lineaarse faasiga. Matemaatiliselt, kui $\{x_{n}\}$ tähistab vektorit x, siis

kui ${\mathcal {F}}(\{x_{n}\})_{k}=X_{k}$

siis ${\mathcal {F}}(\{x_{n}\cdot e^{{\frac {2\pi i}{N}}nm}\})_{k}=X_{k-m}$

ja ${\mathcal {F}}(\{x_{n-m}\})_{k}=X_{k}\cdot e^{-{\frac {2\pi i}{N}}km}$

Ringkonvolutsiooni teoreem ja ristkorrelatsiooni teoreem

Konvolutsiooni teoreem diskreetse Fourier' teisenduse jaoks näitab, et kahe lõpmatu jada konvolutsiooni võib saada kahe üksiku teisenduse tulemuste pöördteisendusest. Kui järjestused on piiratud pikkustega N, siis tekib oluline lihtsustamine. Kui vaadelda DTF-d ja pöörd-DTF-d, võib seda kirjutada järgmiselt:

${\mathcal {F}}^{-1}\left\{\mathbf {X\cdot Y} \right\}_{n}\ =\sum _{l=0}^{N-1}x_{l}\cdot (y_{N})_{n-l}\ \ {\stackrel {\mathrm {def} }{=}}\ \ (\mathbf {x*y_{N}} )_{n}\ ,$

mis on konvolutsioon $\mathbf {x}$ ja $\mathbf {y}$ jadade vahel pikendatud perioodilise liitmisega:

$(\mathbf {y_{N}} )_{n}\ {\stackrel {\mathrm {def} }{=}}\ \sum _{p=-\infty }^{\infty }y_{(n-pN)}=y_{n(modN)}.\,$

Ristkorrelatsioon $\mathbf {x}$  ja  $\mathbf {y_{N}}$  vahel on selline:

${\mathcal {F}}^{-1}\left\{\mathbf {X^{*}\cdot Y} \right\}_{n}=\sum _{l=0}^{N-1}x_{l}^{*}\cdot (y_{N})_{n+l}\ \ {\stackrel {\mathrm {def} }{=}}\ \ (\mathbf {x\star y_{N}} )_{n}\ .$

Konvolutsiooni teoreemi duaalsus

Võib ka tõestada, et:

${\mathcal {F}}\left\{\mathbf {x\cdot y} \right\}_{k}\ {\stackrel {\mathrm {def} }{=}}\sum _{n=0}^{N-1}x_{n}\cdot y_{n}\cdot e^{-{\frac {2\pi i}{N}}kn}={\frac {1}{N}}(\mathbf {X*Y_{N}} )_{k},\,$ mis on ringikujuline konvolutsioon $\mathbf {X}$ ja $\mathbf {Y}$ vahel.

Trigonomeetriline interpolatsiooni polünoom

$p(t)={\frac {1}{N}}\left[X_{0}+X_{1}e^{2\pi it}+\cdots +X_{N/2-1}e^{(N/2-1)2\pi it}+X_{N/2}\cos(N\pi t)+X_{N/2+1}e^{(-N/2+1)2\pi it}+\cdots +X_{N-1}e^{-2\pi it}\right]$ paaris N-i jaoks,

$p(t)={\frac {1}{N}}\left[X_{0}+X_{1}e^{2\pi it}+\cdots +X_{\lfloor N/2\rfloor }e^{\lfloor N/2\rfloor 2\pi it}+X_{\lfloor N/2\rfloor +1}e^{-\lfloor N/2\rfloor 2\pi it}+\cdots +X_{N-1}e^{-2\pi it}\right]$ paaritu N-i jaoks,

kus koefitsiendid X_k on eespool oleva x_n DFT ja rahuldavad interpoleerimist $p(n/N)=x_{n}$ $n=0,\ldots ,N-1$ jaoks.

Paaris N-i puhul tuleb tähele panna, et Nyquist komponenti ${\frac {X_{N/2}}{N}}\cos(N\pi t)$ käsitletakse eraldi.

Ühtne DFT

Teise võimalusena saab DFT-d väljendada DFT maatriksi abil ehk Vandermonde maatriksina, mille võttis kasutusele Sylvester 1867. aastal.

$\mathbf {F} ={\begin{bmatrix}\omega _{N}^{0\cdot 0}&\omega _{N}^{0\cdot 1}&\ldots &\omega _{N}^{0\cdot (N-1)}\\\omega _{N}^{1\cdot 0}&\omega _{N}^{1\cdot 1}&\ldots &\omega _{N}^{1\cdot (N-1)}\\\vdots &\vdots &\ddots &\vdots \\\omega _{N}^{(N-1)\cdot 0}&\omega _{N}^{(N-1)\cdot 1}&\ldots &\omega _{N}^{(N-1)\cdot (N-1)}\\\end{bmatrix}}$

kus

$\omega _{N}=e^{-2\pi i/N}\,$

on primitiivne N-is ühe juur.

Pöördteisendus on selle maatriksi pöördmaatriks:

$\mathbf {F} ^{-1}={\frac {1}{N}}\mathbf {F} ^{*}$

Ühtse normaliseerimise konstantidega $1/{\sqrt {N}}$ saab DFT ühtseks teisenduseks, mis on defineeritud ühtse maatriksi abil:

$\mathbf {U} =\mathbf {F} /{\sqrt {N}}$

$\mathbf {U} ^{-1}=\mathbf {U} ^{*}$

$|\det(\mathbf {U} )|=1$

kus det() on maatriksi determinant. Determinant on omaväärtuste tulemus, mis on kas $\pm 1$ või $\pm i$. Ortogonaalsust väljendab nüüd ortonormaalsuse tingimus.

$\sum _{m=0}^{N-1}U_{km}U_{mn}^{*}=\delta _{kn}$

Kui X on ühtne vektori x DFT, siis

$X_{k}=\sum _{n=0}^{N-1}U_{kn}x_{n}$

ja Planchereli teoreem on väljendatud niimoodi:

$\sum _{n=0}^{N-1}x_{n}y_{n}^{*}=\sum _{k=0}^{N-1}X_{k}Y_{k}^{*}$

Erijuhul $\mathbf {x} =\mathbf {y}$ on see Parsevali teoreem

$\sum _{n=0}^{N-1}|x_{n}|^{2}=\sum _{k=0}^{N-1}|X_{k}|^{2}$

Pöördvõrdelise DFT avaldamine DFT kaudu

Kasulik DFT omadus on see, et pöördteisendust saab kergesti väljendada tavalise DFT kaudu, kasutades allolevaid nippe:

Esiteks saame arvutada pöördvõrdeline DFT, pöörates vastupidi kõik peale ühe sisendi.

${\mathcal {F}}^{-1}(\{x_{n}\})={\mathcal {F}}(\{x_{N-n}\})/N$

Teiseks võib ka ümber pöörata sisendid ja väljundid:

${\mathcal {F}}^{-1}(\mathbf {x} )={\mathcal {F}}(\mathbf {x} ^{*})^{*}/N$

Viimaseks võime vahetada omavahel reaal- ja imaginaarsignaali osad:

${\mathcal {F}}^{-1}(\mathbf {x} )={\textrm {swap}}({\mathcal {F}}({\textrm {swap}}(\mathbf {x} )))/N$

Kus swap($x_{n}$) on $x_{n}$, milles on reaal- ja imaginaar-osad omavahel niimoodi vahetatud: $x_{n}=a+bi$ swap($x_{n}$) on $b+ai$. Samas, swap($x_{n}$) on võrdne $ix_{n}^{*}$.

Omaväärtused ja omavektorid

DFT maatriksi omaväärtused on lihtsad ja hästi tuntud, kusjuures omavektorid on keerulised ja neid pole veel täiesti uuritud.

Kui DFT ühtne vorm $\mathbf {U}$ pikkusega N on selline:

$\mathbf {U} _{m,n}={\frac {1}{\sqrt {N}}}\omega _{N}^{(m-1)(n-1)}={\frac {1}{\sqrt {N}}}e^{-{\frac {2\pi i}{N}}(m-1)(n-1)}.$

See maatriks vastab maatriksite polünomiaalsele võrrandile:

$\mathbf {U} ^{4}=\mathbf {I} .$

See tähendab, et omaväärtused $\lambda$ võrrandile on:

$\lambda ^{4}=1.$

Samas on $\mathbf {U}$ omaväärtused neljandad ühe juured: $\lambda$ on +1, −1, +i, või −i.

Kuna on olemas ainult neli omaväärtust, siis need omavad mitmesust, mis annab omavektorite numbri igale omaväärtusele.

Paljususe probleemi lahendasid McClellan ja Parks, samas ekvivalentse probleemi lahendas varem Gauss. Mitmesus sõltub absoluutväärtusest N ja on näidatud järgmises tabelis:

suurus N	λ = +1	λ = −1	λ = -i	λ = +i
4m	m + 1	m	m	m − 1
4m + 1	m + 1	m	m	m
4m + 2	m + 1	m + 1	m	m
4m + 3	m + 1	m + 1	m + 1	m

Määramatuse printsiip

Kui juhuslik suurus X_k on piiratud:

$\sum _{n=0}^{N-1}|X_{n}|^{2}=1~,$

siis

$P_{n}=|X_{n}|^{2}$

võib esindada diskreetse tõenäosuse n-i massi-funktsiooni koos tõenäosuse massi-funktsiooni funktsiooniga, mis on saadud transformeeritud muutujast,

$Q_{m}=N|x_{m}|^{2}~.$

Pidevate funktsioonide $P(x)$ ja $Q(k)$ jaoks väidab Heisenbergi määramatuse printsiip, et

$D_{0}(X)D_{0}(x)\geq {\frac {1}{16\pi ^{2}}}$

kus $D_{0}(X)$ ja $D_{0}(x)$ on $|X|^{2}$ ja $|x|^{2}$ erinevused, koos võrdsusega, mis on saavutatud sobivalt normaliseeritud Gaussi jaotusest.

Hirschmanni entroopialine ebakindlus omab kasulikku analoogi ka DFT puhul. Hirschmani määramatuse printsiip on väljendatud Shannoni entroopia poolest kahe tõenäosusfunktsiooni abil.

Diskreetsel juhul on Shannoni entroopiad

$H(X)=-\sum _{n=0}^{N-1}P_{n}\ln P_{n}$

ja

$H(x)=-\sum _{m=0}^{N-1}Q_{m}\ln Q_{m}~,$

ja entroopialine määramatuse printsiip muutub

$H(X)+H(x)\geq \ln(N)~.$

Reaalse sisendiga DFT

Kui $x_{0},\ldots ,x_{N-1}$ on reaalarvud, nagu nad on tavalises olukorras, siis DFT allub sümmeetriale:

$X_{N-k}\equiv X_{-k}=X_{k}^{*},$  kus $X^{*}\,$ tähendab kompleksset konjugatsiooni.

X₀ ja X_N/2 on reaalsed väärtused ja ülejäänud DFT on täielikult määratud ainult N/2-1 kompleksarvudega.

Üldistatud DFT (nihkunud ja mittelineaarne faas)

On võimalik nihutada teisenduse proovivõttu aja ja/või sageduspiirkonna mingi a ja b väärtuse võrra. Seda nimetatakse tavaliselt üldistatud DFT-ks (GDFT inglise keeles) või nihutatud DFT-ks. Üldistatud DFT omab analoogsed omadusi nagu tavaline DFT:

$X_{k}=\sum _{n=0}^{N-1}x_{n}e^{-{\frac {2\pi i}{N}}(k+b)(n+a)}\quad \quad k=0,\dots ,N-1.$

Kõige tihedamini kasutatakse nihet $1/2$ proovi võrra. Tavaline DFT vastab perioodilisele signaalile nii aja kui ka sageduse domeenis, $a=1/2$ $(b=1)$ esitab vastu perioodilist signaali ($X_{k+N}=-X_{k}$) ja vastupidi, kui $b=1/2$ $(a=1)$. On olemas ka erijuht $a=b=1/2$, mida on nimetatud paaritu aja ja sagedusega DFT-ks (O² DFT inglise keeles). Selliseid teisendusi kasutatakse sümmeetriliste signaalide puhul, et esitada erinevaid piirsümmeetriad. Reaalsignaalide puhul vastavad need erinevatele siinus- ja koosinus-signaalidele.

Teine huvitav juhtum on, kui $a=b=-(N-1)/2$, mida nimetatakse tsentreeritud DFT-ks (CDFT inglise keeles). See DFT omab kasulikku omadust: kui N on nelja korrutis, siis kõik neli tema ühisväärtust omavad võrdset mitmesust.

Diskreetset Fourier' teisendust võib vaadelda z-teisenduse erijuhuna, mida hinnatakse ühikringil komplekstasandil; z-teisendused vastavad kompleksnihetele a ja b, nagu on näidatud eespool.

Mitmemõõtmeline DFT

Tavaline DFT tegeleb ühemõõtmelisega andmete massiiviga $x_{n}$ kuna see on funktsioon täpselt ühe diskreetse muutujaga n. Mitmemõõtmeline DFT tegeleb mitmemõõtmelise massiiviga $x_{n_{1},n_{2},\dots ,n_{d}}$ ja avaldub d diskreetsete muutujatega funktsiooniks $n_{\ell }=0,1,\dots ,N_{\ell }-1$ iga $\ell$ $1,2,\dots ,d$ sees on defineeritud:

$X_{k_{1},k_{2},\dots ,k_{d}}=\sum _{n_{1}=0}^{N_{1}-1}\left(\omega _{N_{1}}^{~k_{1}n_{1}}\sum _{n_{2}=0}^{N_{2}-1}\left(\omega _{N_{2}}^{~k_{2}n_{2}}\cdots \sum _{n_{d}=0}^{N_{d}-1}\omega _{N_{d}}^{~k_{d}n_{d}}\cdot x_{n_{1},n_{2},\dots ,n_{d}}\right)\right)\,,$

kus $\omega _{N_{\ell }}=\exp(-2\pi i/N_{\ell })$ ja d väljundi indeksid on $k_{\ell }=0,1,\dots ,N_{\ell }-1$. Natuke kompaktsemalt on see väljendatud kui vektor, kus $\mathbf {n} =(n_{1},n_{2},\dots ,n_{d})$ ja $\mathbf {k} =(k_{1},k_{2},\dots ,k_{d})$ on d-mõõtmelised vektorid indeksitega nullist $\mathbf {N} -1$, kus $\mathbf {N} -1=(N_{1}-1,N_{2}-1,\dots ,N_{d}-1)$:

$X_{\mathbf {k} }=\sum _{\mathbf {n} =\mathbf {0} }^{\mathbf {N} -1}e^{-2\pi i\mathbf {k} \cdot (\mathbf {n} /\mathbf {N} )}x_{\mathbf {n} }\,,$

kus $\mathbf {n} /\mathbf {N}$ on $\mathbf {n} /\mathbf {N} =(n_{1}/N_{1},\dots ,n_{d}/N_{d})$ ja summa tähistab pesastatud summeerimist üleval olevas valemis.

Pöördvõrdeline mitmemõõtmeline DFT avaldub samamoodi nagu ühe mõõtme korral:

$x_{\mathbf {n} }={\frac {1}{\prod _{\ell =1}^{d}N_{\ell }}}\sum _{\mathbf {k} =\mathbf {0} }^{\mathbf {N} -1}e^{2\pi i\mathbf {n} \cdot (\mathbf {k} /\mathbf {N} )}X_{\mathbf {k} }\,.$

DFT väljendab sisendit $x_{n}$ sinusoidide superpositsiooniga, mitmemõõtmeline DFT väljendab sisendit tasandi lainete superpositsiooniga, või mitmemõõtmeliste sinusoididega. Ostsillatsiooni suund on $\mathbf {k} /\mathbf {N}$ ja amplituudid on $X_{\mathbf {k} }$. See lagunemine omab suurt tähtsust paljudel aladel, alustades digitaalsest pilditöötlusest (kahemõõtmeline) kuni diferentsiaalvõrrandite lahendamiseni. Tulemus on jagatud tasandite lainetele.

Mitmemõõtmeline DFT võib olla arvutatud kui iga mõõtme ühemõõtmelise DFT-de kompositsioon. Kahemõõtmelise DFT puhul $x_{n_{1},n_{2}}$ on $N_{1}$sõltumatu ridade DFT-d (näiteks mööda $n_{2}$) arvutatud esimesena uueks massiiviks $y_{n_{1},k_{2}}$. Järgmisena $N_{2}$ sõltumatu veergude DFT-d (mööda $n_{1}$) arvutatakse, et saada lõpptulemust $X_{k_{1},k_{2}}$. Võib teha ka vastupidi ja esimesena arvutada veerud ja pärast read. Järjekord pole oluline, sest lõpus arvutatakse pesastatud summa.

Ühemõõtmelise DFT arvutamise algoritm on piisav selleks, et arvutada ka mitmemõõtmelised DFT-d. Selle algoritmi nimetuseks on rea-veeru algoritm. On olemas ka mõned teised algoritmid mitmemõõtmeliste DFT-de arvutamiseks.

Reaalse sisendiga mitmemõõtmeline DFT

Kui sisend koosneb reaalsetest arvudest $x_{n_{1},n_{2},\dots ,n_{d}}$, DFT väljund omab konjugatiivset sümmeetriat nagu ühemõõtmelisel juhul:

$X_{k_{1},k_{2},\dots ,k_{d}}=X_{N_{1}-k_{1},N_{2}-k_{2},\dots ,N_{d}-k_{d}}^{*},$

kus tärn tähendab kompleksset konjugatsiooni ja $\ell$-is indeks on absoluutväärtus $N_{\ell }$ (iga $\ell =1,2,\ldots ,d$ jaoks).

Kiire DFT

Kiire Fourier' teisendus (Fast Fourier Transform = FFT) põhineb teisendamiseks vajalike arvutuste mahu vähendamisel teatud (korduvate) tulemuste (korduva) ärakasutamise teel või mõne spetsiifilise vaheteisenduse kasutamise teel. Seetõttu on FFT reeglina kasutatav vaid diskreeditud funktsioonide ja signaalide puhul. Siiski on ka analoogtehnikas mõned signaalitöötluse võtted vaadeldavad kui FFT teatud vormid.

FFT kasutatavusse ja FFT abil saadud tulemustesse tuleb seetõttu suhtuda vajaliku kriitilisusega, kuna lisaks diskreetmisest tulenevatele iseärasustele tuleb lisaks arvesse võtta veel ka FFT enda olemusest tulenevaid iseärasusi (lühike ajaintervall ja sellest tulenevalt nn. vaatluse akna(funktsiooni) kasutamine, sünkroonsuse probleemid).

FFT kasutatavus on praktikas laialdane (heli- ja sidetehnika, jm), kuna paljudel juhtudel suurt täpsust selle mõõtetehnilises mõttes ei nõuta (heli puhul loetakse piisavaks 1dB ehk ~10% täpsust). Arvutuse täpsuse probleemid on aga üldjuhul lahendatavad.

Kiire DFT arvutamiseks kasutatakse mitu algoritmi: Cooley-Tukey FFT, Prime-factor FFT, Bruun's FFT, Rader's FFT, ja Bluestein's FFT.

Rakendused

DFT on kasutatud paljudel aladel ja siin on näidatud ainult tähtsamad neist. Peaaegu kõik DFT rakendused otseselt põhinevad sellel põhimõttel, et DFT-d ja pöörd-DFT on võimalik efektiivselt arvutada Kiire Fourier' teisenduse abil .

Spektraalanalüüs

Kui DFT-d kasutatakse spektraalanalüüsiks, siis $\{x_{n}\}\,$ jada tavaliselt kujutab piiratud koguse ühtlaste aja vahedega paigutatud mingi signaali proove $x(t)\,$, kus t on aeg. Üleminek pidevalt ajalt proovidele muudab $x(t)\,$ Fourier' teisendust Diskreetse aja Fourier teisenduseks (DTFT), mis tavaliselt tähendab deformeerimist (aliasing inglise keeles). Deformeerimise minimeerimiseks tuleb õigesti valida proovide võitmise sagedust, arvestades Nyquist-i sagedust. Samas, tuleb proovide jada konverteerida väga suurest(või lõpmatust) sobivaks, et vältida teist deformeerimist, nimetatud lekkimine, ehk resolutsiooni kaotamine DFT-s. Kui kättesaadav andmete hulk on liiga väike, või andmete töötlemiseks (vajaliku resolutsiooni leidmiseks) pole piisavalt aega, kasutatakse mitu DFT-d spektrogrammi tegemiseks. Tulemusena on võimsuse spekter kus esineb müra ja/või juhuslikud andmed, mida saab filtreerida mitu DFT tulemuste võrdlemisega. See protseduur vähendab spektri dispersiooni ja on nimetatud perioodgrammiks. Tuntud näited selle meetodi kasutamisest on Welchi ja Bartletti meetodid. Üldine meetod võimsuse spektri hindamiseks lärmaka signaali puhul on nimetatud spektraalne hindamine.

DFT ise on lõplik moonutamise allikas, sest DFT on ainult diskreetne proovide võtmine pidevast funktsioonist. Seda on võimalik leevendada DFT resolutsiooni suurendamisega.

Andmete pakkimine

Digitaalse signaalitöötluse valdkond põhineb sagedusdomeenis toimuvates operatsioonides (Fourier' teisenduse tulemustes). Näiteks andmekaostega piltide töötlus ja heli pakkimise meetodid kasutavad DFT-d: signaal on lõigatud lühikesteks segmentideks (proovide võtmine), iga lõik on transformeeritud, ja siis peaaegu märkamatu kõrgesageduslikud Fourier' koefitsiendid, kõrvaldatakse. Dekompressor arvutab pöördtransformatsiooni, mis põhineb uutel DFT väärtustel. Pakkimise rakendused kasutavad sageli spetsialiseeritud DFT vormi, diskreetse koosinus teisendust, või juba seda modifitseeritud versiooni. Mõned suhteliselt hiljutised kokkupakkimisalgoritmid kasutavad nn laineke teisendust, mis annab ühtlasema kompromissi aja ja sageduse domeenide vahel. JPEG2000 juhul, see väldib vigaste piltide tekkimist, mis ilmuvad, kui pildid on liiga palju tihendatud algse JPEG pakkimise tõttu.

Osatuletistega diferentsiaalvõrrandid

Diskreetne Fourier' teisendust kasutatakse sageli osatuletistega diferentsiaalvõrrandite ahendamisel, kus DFT-d kasutatakse Fourier' rea liigikaudseks arvutamiseks. Selle lähenemise eeliseks on see, et signaali laiendatakse kompleks eksponentideks $e^{inx}$, mis on diferentseerimise tulemuste funktsioonide hulk: ${{\text{d}}{\big (}e^{inx}{\big )}}/{\text{d}}x=ine^{inx}$. Seega Fourier' esindamises, diferentseerimine on lihtne – see on korrutamine väärtusega $in$. Lineaarne diferentsiaalvõrrand konstantsete kordajatega muundub kergesti lahendatavaks algebraliseks võrrandiks. Tulemuse tagasi aja domeeni teisendamiseks tuleb kasutada pöörd teisendust. Seda ka nimetatakse spektraalmeetodiks ehk spektraalanalüüsiks.

Polünoomiline korrutamine

Oletame, et me soovime arvutada polünoomi c(x) = a(x) · b(x). Tavaline koefitsientide c väljend hõlmab lineaarset (atsüklilist) konvolutsiooni. Seda saab kirjutada tsüklilise konvolutsiooni kasutades, kui võtta koefitsient vektoriteks a(x) ja b(x) pideva väljendiga esimeseks, seejärel lisades nulle nii, et tulemus koefitsient vektorid a ja b on mõõtmes d > deg(a(x)) + deg(b(x)). Siis,

$\mathbf {c} =\mathbf {a} *\mathbf {b}$

Kus c on koefitsientide vektor c(x), ja konvolutsiooni operaator $*\,$ on

$c_{n}=\sum _{m=0}^{d-1}a_{m}b_{n-m\ \mathrm {mod} \ d}\qquad \qquad \qquad n=0,1\dots ,d-1$

Aga konvolutsioon muutub korrutamiseks DFT all:

${\mathcal {F}}(\mathbf {c} )={\mathcal {F}}(\mathbf {a} ){\mathcal {F}}(\mathbf {b} )$

Siin on vektor võetud elemendi kaupa. Seega polünoomi koefitsiendid c(x) on vaid 0, ..., deg(a(x)) + deg(b(x)) ja koefitsient vektorist on

$\mathbf {c} ={\mathcal {F}}^{-1}({\mathcal {F}}(\mathbf {a} ){\mathcal {F}}(\mathbf {b} )).$

Kiire DFT algoritmi kasutuses ajaline keerukus on O (N log N). Teisenduse operatsiooni jaoks tavaliselt kasutatakse Cooley-Tukey FFT algoritmi, sest see on lihtne ja suhteliselt kiire. Sel juhul peab $d$ olema väiksem täisarv, mis on suurem, kui sisend-polünoomi algtegurite summa.

Suurte täisarvude korrutamine

Kõige kiirem tuntud algoritmidest väga suurte täisarvude korrutamiseks on polünoomide korrutamise meetod. Täisarve võib käsitleda, kui polünoomide väärtused väärtustatud konkreetse arvu alusel, koos polünoomi koefitsientidega, mis on selle arvu numbrid. Pärast polünoomilist korrutamist lõpetab korrutamise suhteliselt väikese keerukusega nn carry-paljundamine.

Konvolutsioon

Kuna konvolutsioon on sagedus domeenis lihtsalt korrutamine, siis palju lihtsam on teisendada sisendid DFT abil, järgmisena teha korrutist ja viimasena teisendada tulemust pöördteisendusega tagasi aja domeeni.

Olulised DFT paarid

$x_{n}={\frac {1}{N}}\sum _{k=0}^{N-1}X_{k}e^{i2\pi kn/N}$	$X_{k}=\sum _{n=0}^{N-1}x_{n}e^{-i2\pi kn/N}$	Nimetus
$x_{n}e^{i2\pi n\ell /N}\,$	$X_{k-\ell }\,$	Nihe
$x_{n-\ell }\,$	$X_{k}e^{-i2\pi k\ell /N}\,$
$x_{n}\in \mathbb {R}$	$X_{k}=X_{N-k}^{*}\,$	Reaalne DFT
$a^{n}\,$	$\left\{{\begin{matrix}N&{\mbox{if }}a=e^{i2\pi k/N}\\{\frac {1-a^{N}}{1-a\,e^{-i2\pi k/N}}}&{\mbox{mujal}}\end{matrix}}\right.$	Geomeetriline progressioon
${N-1 \choose n}\,$	$\left(1+e^{-i2\pi k/N}\right)^{N-1}\,$	Binominaalne teoreem
$\left\{{\begin{matrix}{\frac {1}{W}}&{\mbox{if }}2n<W{\mbox{ or }}2(N-n)<W\\0&{\mbox{mujal}}\end{matrix}}\right.$	$\left\{{\begin{matrix}1&{\mbox{if }}k=0\\{\frac {\sin \left({\frac {\pi Wk}{N}}\right)}{W\sin \left({\frac {\pi k}{N}}\right)}}&{\mbox{mujal}}\end{matrix}}\right.$	$x_{n}$ on W punktiline ristkujuline aknafunktsioon keskpunktiga n=0, kus W on paaritu reaalarv, ja $X_{k}$ on sinc funktsioon.
$\sum _{j\in \mathbb {Z} }\exp \left(-{\frac {\pi }{cN}}\cdot (n+N\cdot j)^{2}\right)$	${\sqrt {cN}}\cdot \sum _{j\in \mathbb {Z} }\exp \left(-{\frac {\pi c}{N}}\cdot (k+N\cdot j)^{2}\right)$	Skaleeritud Gaussi funktsioonide diskreetimine ja perioodiline liitmine, kus $c>0$.

Üldistused

Esinduse teooria

DFT-d võib tõlgendada kui kompleksset piiratud tsüklilise rühma esinduse teooriat. Teisisõnu, n kompleksarvude jada võib olla tõlgendatud nägu n-mõõtmeline kompleksne ruum Cⁿ või lõplikku tsüklilise kompleksarvude rühma funktsioon f, Z_n → C. f on tsükliline piiratud rühma klassi funktsioon, ning seda saab väljendada taandumatu tähemärkide lineaarse kombinatsioonina selles rühmas. Need märgid on ühe juured.

Muud valdkonnad

Palju DFT omadustest sõltuvad ainult sellest, et $e^{-{\frac {2\pi i}{N}}}$ on primitiivsed ühe juured. Need omadused on täielikkus, ortogonaalsus, Plancherel/Parseval, perioodilisus, nihe, konvolutsioon ja paljud kiire DFT algoritmid. Seetõttu DFT-d võib defineerida ühe juure mõiste kasutades ka muudes valdkondades. Neid üldistusi tavaliselt nimetatakse number-teoreetilised teisendused (number-theoretic transforms (NTT)).

Muud piiratud rühmad

Tavaline DFT tegeleb x₀, x₁, …, x_N−1 kompleksarvude jadaga, mis võib olla vaadeldud funktsioonina {0, 1, …, N − 1} → C. Mitmemõõtmeline DFT tegeleb mitmemõõtmeliste jadadega, mis võivad olla vaadeldud funktsioonidena

$\{0,1,\ldots ,N_{1}-1\}\times \cdots \times \{0,1,\ldots ,N_{d}-1\}\to \mathbb {C} .$

Siis tavalist DFT-d vaadeldakse tsüklilise rühma Fourier' teisendusena, ja mitmemõõtmeline DFT on tsükliliste rühmade summa Fourier' teisendus.

Välislingid

• Interactive explanation of the DFT
• Matlab tutorial on the Discrete Fourier Transformation
• Interactive flash tutorial on the DFT
• Mathematics of the Discrete Fourier Transform by Julius O. Smith III
• FFTW: Fast implementation of the DFT - coded in C and under General Public License (GPL)
• General Purpose FFT Package: Yet another fast DFT implementation in C & FORTRAN, permissive license
• Explained: The Discrete Fourier Transform