Laurent'i rida
Laurent'i rida on kompleksmuutuja funktsiooni esitus astmereana, mis sisaldab ka negatiivseid astendajaid.
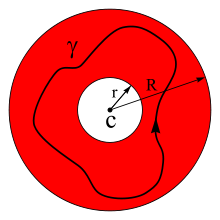
See on nimetuse saanud prantsuse matemaatiku Pierre Alphonse Laurent'i järgi, kes selle aastal 1843 avaldas.
Definitsioon
muudaKompleksmuutuja funktsiooni f(z) Laurent'i rida punkti c suhtes on:
kus kordajad an on antud joonintegraalina:
Viimane avaldis on Cauchy integraalvalemi üldistus. Integraali raja γ on vastupäeva suunatud pidev suletud joon, mis ümbritseb punkti c ja paikneb rõngal, kus f(z) on regulaarne. f(z) rittaarendus kehtib kõikjal rõnga sisemuses.