Huffmani kodeerimine
Huffmani kodeerimine on prefikskoodide üks liik. Huffmani kodeerimise idee on asendada olemasolev sümboleid kirjeldav bitijada ümber nõnda, et informatsiooni hulgas tihemini esinevad tähemärgid saaksid kirjeldatud lühema bitijadaga. Tulemuseks on informatsiooni kirjeldus esinemistihedust eelistaval ja minimaalset tähemärkide hulka kasutaval alusel. Informatsiooni kirjeldav andmehulk ei pruugi väheneda ja võib eriolukorras isegi kasvada, kuid tegemist on tihendusalgoritmiga, mis tavateksti pakkimisel saavutab märgatava erinevuse (tihti üle 30%).
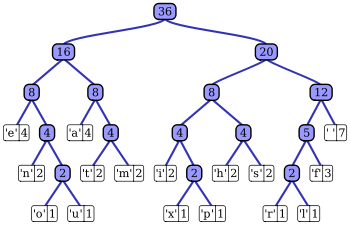
Algoritmi rakendamine
muudaHuffmani kodeerimisalgoritm põhineb konkreetse informatsiooni tähemärkide sageduse põhjal binaarpuu ehitamisel ja sellest tähemärkide bitijada kirjeldava kodeerimistabeli loomisel. Faili tihendamise puhul kirjeldatakse väljundfaili puud ja algse sisendfaili sisu. Tähemärgid asendatakse uue kodeeringuga.
Otsese informatsiooni sisaldava faili tihendamisel on mõned lahendamist vajavad kitsaskohad. Näiteks tuleb teha väljundfaili lõpu tuvastus, sest tõenäoliselt ei lõpe fail baidi pealt, vaid selles on mõnebitine ülejääk.
Binaarpuu rakendamiseks kasutatav struktuur
muuda//tüüpiline struktuur programmeerimskeeles C, mida kasutada binaarpuu ehitamisel
typedef struct tree {
int ch; //tähemärgi numbriline kood
int freq; //informatsioonis esinemise tihedus
struct tree *left; //viide sama tüüpi struktuurile
struct tree *right; //2 viide sama tüüpi struktuurile
} tree;
Puu ehitamisel kasutatavad mõisted
muuda- Leht – element, mille tähemärgi numbrikood on määratud positiivselt, harud jäävad ühendamata (tal pole neid).
- Vars – element, mille tähemärgi numbrikood on vaid algväärtustatud, harud on väärtustatud, esinemistihedus on varre harudes olevate elementide esinemistiheduse summa.
- Juur – element, mille harusid pidi võib jõuda kõigi lehtedeni.
- Haru – elemendi viide sama tüüpi elemendile.
- Luuakse lehtede massiiv, milles on tähemärgid ja nende esinemissagedused.
- Massiiv sorditakse esinemissageduse alusel.
- Luuakse uus vars, mille harud ühendatakse kahe väiksema esinemissagedusega elemendiga massiivis.
- Massiivi lisatakse vars ja eemaldatakse selle harudes asetsevad elemendid.
- Lisatud varre esinemissageduseks määratakse selle harudes olevate elementide summa.
- Kui massiivis on järgi vaid üks element, on puu valmis, kui mitte, korratakse algoritmi alates punktist 2.
Kodeerimistabeli loomise rekursiivne algoritm
muuda- Saadakse viit puu juurele.
- Kui tegemist on lehega, lisatakse kodeerimistabelisse loodud kood ja koodi pikkus.
- Kui varrel on vasakpoolne (esimene) haru olemas, pikendatakse koodi ja pöördutakse punkti 1.
- Kui varrel on parempoolne (teine) haru olemas, määratakse koodi viimane bitt 1ks, pikendatakse koodi ja pöördutakse punkti 1.
Tõenäoliselt pole raske iteratiivset algoritmi luua, kuid seda pole vaja, sest tähed on üldjuhul kirjeldatud 8 bitiga, mille kõigi kombinatsioonide hulk on 256.
Kodeerimistabeli näide
muudaKodeerimistabeli element koosneb vormist ja pikkusest ning kõik elemendid saavad pärast seda algoritmi määratud unikaalsete bitijadadega. Allpool on tabel eelneva ja uue kodeeringu erinevustest. Kodeerimistabeli informatsiooniks on sõne "this is an example of a huffman tree".
Kodeerimistabel: Tähemärk ' ' nr(32) | binaarkood:00100000 | uus binaarkood:111 Tähemärk 'a' nr(97) | binaarkood:01100001 | uus binaarkood:001 Tähemärk 'e' nr(101) | binaarkood:01100101 | uus binaarkood:000 Tähemärk 'f' nr(102) | binaarkood:01100110 | uus binaarkood:1101 Tähemärk 'h' nr(104) | binaarkood:01101000 | uus binaarkood:1100 Tähemärk 'i' nr(105) | binaarkood:01101001 | uus binaarkood:1001 Tähemärk 'l' nr(108) | binaarkood:01101100 | uus binaarkood:01101 Tähemärk 'm' nr(109) | binaarkood:01101101 | uus binaarkood:1000 Tähemärk 'n' nr(110) | binaarkood:01101110 | uus binaarkood:1011 Tähemärk 'o' nr(111) | binaarkood:01101111 | uus binaarkood:01100 Tähemärk 'p' nr(112) | binaarkood:01110000 | uus binaarkood:01111 Tähemärk 'r' nr(114) | binaarkood:01110010 | uus binaarkood:01110 Tähemärk 's' nr(115) | binaarkood:01110011 | uus binaarkood:1010 Tähemärk 't' nr(116) | binaarkood:01110100 | uus binaarkood:0101 Tähemärk 'u' nr(117) | binaarkood:01110101 | uus binaarkood:01001 Tähemärk 'x' nr(120) | binaarkood:01111000 | uus binaarkood:01000
Vaata ka
muudaVälislingid
muuda| Pildid, videod ja helifailid Commonsis: Huffmani kodeerimine |
- Program for explaining the Huffman Coding procedure.
- Huffman Code Applet
- n-ary Huffman Template Algorithm
- Sloane A098950 Minimizing k-ordered sequences of maximum height Huffman tree
- Computing Huffman codes on a Turing Machine
- Mordecai J. Golin, Claire Kenyon, Neal E. Young "Huffman coding with unequal letter costs" (PDF), STOC 2002: 785-791
- Huffman Coding: A CS2 Assignment a good introduction to Huffman coding
- A quick tutorial on generating a Huffman tree
- Pointers to Huffman coding visualizations
- Huffman in C
- Huffman in Java
- Huffman binary algorithm applet
- Implementation approaches to Huffman Decoding