Sümmeetria
| See artikkel räägib üldmõistest ning sümmeetriast filosoofias; muude tähenduste kohta vaata Sümmeetria (täpsustus) |
Sümmeetria (kreeka sõnast συμμετρία – koosmõõtuvus) on laiemas tähenduses määratletav kui ühetaolisus, proportsionaalsus, tasakaal, vastavus või püsivus. Täpsemalt defineeritud kui struktuurne omadus, mis avaldub objekti ühetaoliste osade ühtlases kordumises nii ruumis kui ka ajas. [1]

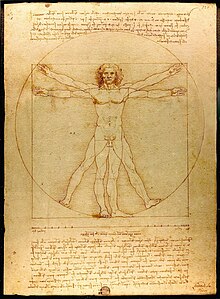
Levinud on arusaam sümmeetriast kui paarsusest – sümmeetria on objekti omadus, kus selle mingist keskpunktist või sümmeetriateljest samal kaugusel olevad osad on ühetaolised [2].
Sümmeetriailminguid esineb nii ühiskonnas kui ka elusas ja elutus looduses. Ideaalselt sümmeetriline objekt on kera.
Sümmeetria juured muuda
Sümmeetria on looduse ilming, kus selle objektide sümmeetria on tingitud fundamentaalsetest loodusseadustest:
A) Taimsete objektide vertikaalne asend on gravitatsiooni poolt esile kutsutud korrastatud jaotumine ruumis, kus taimede võra tasakaalustab nende juurestik. Loomne olend aga peab tasakaalu hoidmiseks ja liikumiseks omama keskmest kahele poole väljaulatuvaid paarisarv jäsemeid, mis teeb selle bilateraalselt sümmeetriliseks.
B) Kordumised ehk korrastatud jaotumine ajas on üks esimesi looduslikke sümmeetriailminguid mitmesuguste astronoomiliste, klimaatiliste jt tsüklite näol.
Mikro- ja makromaailmas võivad selleks olla ka teised jõud ja teistsugused tsüklid.
Bilateraalset looduslikku sümmeetriat kujutasid oma ornamentidel ja gravüüridel juba vanad sumerid 3. aastatuhandel eKr. Korrastatud jaotumise vastu ajas ehk astronoomiliste tsüklite vastu huvituti Vana-Indias juba 5. aastatuhandel eKr.
Sümmeetria mitmepalgelisus muuda
See mitmepalgelisus avaldub eelkõige lahknevuses korrastatud jaotumises ruumis ja ajas. Sümmeetriat võib täheldada seega ajas, ruumilistes suhetes, geomeetrilistes teisendustes nagu peegeldus ja pöörded, mitmesugustes abstraktsetes mudelites, keeles ja muusikas. Sümmeetrilised objektid esinevad nii materiaalsel kujul, nagu elusisendid, kristallid või esemed, kui ka abstraktsel kujul matemaatiliste konstruktsioonide või helindite jadana.
Eluslooduses on sümmeetria äratuntav peamiselt geomeetriliselt, bilateraalsel ja radiaalsel kujul. Elutus looduses esinevad sümmeetriailmingud mitmel viisil: füüsikas näiteks invariantsuse, jäävusseaduste, tasakaalu või võre näol; keemilise ühendi sümmeetriaomadused on väljaloetavad selle struktuurivalemist või struktuurimudelist. Matemaatikas on sümmeetria määratletud nii ühetaolisuse kui ka vastavuse aspektist: a) Rühmateoorias on sümmeetria määratletud kui elementide transpositsioonide (transitiivsuspiirkonna) ehk orbiidi olemasolu, näiteks graafides. b) Binaarse relatsiooni omadus: relatsioon R on sümmeetriline, kui xRy korral alati ka yRx. [3]. Ka arvtelg on sümmeetriline. Positiivne ja negatiivne osa on nulli suhtes absoluutväärtustena võrdsed.
Sotsiaalias otsitakse sarnasusi ehk sümmeetriat mitmesuguste tunnuste järgi. Kujutavas kunstis esineb sümmeetriat n-ö looduslikul kujul, st bilateraalselt ja radiaalselt kui ka kordumiste näol. Arhitektuuris domineerib geomeetriline sümmeetria (kui seda üldse esineb). Sümmeetriailmingud muusikas avalduvad helindite ja žanriliste kordumiste ning rütmi näol kus oluline osa on ka kontrastidel. Nii on see ka ilukirjanduses, kus need võivad avalduda olukordade ja stseenide sarnasuses ning kordumises, kusjuures poeesias lisanduvad sellele ka riimid. Neid loetelusid võib veelgi jätkata ja täpsustada, kuid piirdugem praegu sellega.
Sümmeetria kui niisugune muuda
Vaatamata sellele, et sümmeetriat on käsitletud paljudest aspektidest, on tegemist siiski sellesama sümmeetriaga, st süsteemis esinevate ühesugusustega, kuigi eri valdkondades võib see ühesugusus kanda erinevaid nimetusi. See ühesugusus tähendab ka vasaku ja parema poole ühesugusust. Liikluses on neid pooli vaja muidugi eristada, kuid see sõltub sellest, kus ja kuidas.
Sümmeetriat tuleb vaadata ka kui lihtsuse ja selguse avaldumise vormi. Albert Einstein tõdes, et loodusele meeldib lihtsus ja looduse mõistmine tähendab lihtsamate matemaatiliste ideede mõistmist.
Sümmeetria kui niisuguse vastu on huvi tundnud eri valdkondade uurijaid. Eriline koht on siin saksa matemaatikul ja filosoofil Hermann Weylil, kes oli veendunud, et olenemata objektist on sümmeetria kujunenud oluliseks matemaatiliseks mõisteks, nii nagu seda on arv, funktsioon või võrrand [4]. Kuid siin peab kohe märkima seda, et paljude eluslooduse objektide sümmeetria ei ole fikseeritav n-ö matemaatilise täpsusega.
Sümmeetria algab siis, kui objektil esineb vähemalt kaks sarnast osist (elementi) ja saavutab täielikkuse siis, kui selle kõik elemendid on sarnased. Ideaalselt sümmeetriline objekt on kera (sfäär), tasapinnal aga ring. Sümmeetria lõpeb seal, kus sarnaseid elemente ei esine, siis on tegemist sümmeetria alumise piiri, asümmeetria ehk 0-sümmeetriaga.
Sümmeetriat kui niisugust on uuritud peamiselt kahel viisil:
- sümmeetriat kui tervikilmingut on uuritud sümmeetriarühmade (teatud tingimustele vastavate hulkade) baasil, nagu seda tegi ka Weyl;
- sümmeetriat kui struktuurset omadust on uuritud struktuurimudelite baasil kus sümmeetriaomadused on esitatud sümmeetriaklasside täpsusega. [5]
Sümmeetria mõõt muuda
Sümmeetria kui struktuurne omadus on mõõdetav vastavate struktuurimudelite baasil. Sümmeetria mõõt sõltub sümmeetriaklasside ehk orbiitide võimsusest ja arvust. Sümmeetria mõõdu lähtealuseks on Shannoni klassikaline infomahu valem:
, kus N on sümmeetriaklasside arv, n sümmeetriaklassi indeks ja pn sümmeetriaklassi osakaal struktuuris.
Saadud suuruse H alusel määratakse objekti sümmeetriamõõt M järgmiselt:
, kus |E| on elementide koguarv struktuuris ning .
Sümmeetriat saab mõõta nii struktuursete elementide kui ka binaarsuhete aspektist. Sümmeetriamõõt on 1, kui esineb üksainus sümmeetriaklass; sümmeetriamõõt on 0, kui sümmeetriaklasside arv võrdub elementide (või binaarsuhete) arvuga. Sümmeetriaväärtused võimaldavad eri suurusega objektide sümmeetriaomadusi võrrelda. Sümmeetriamõõdu M ametlik nimi on korrapära.
Viited muuda
- ↑ Новая философская энтсиклопедия. 2001, Москва. ISBN 5244009613
- ↑ Schmidt, Heirich, 1991. Philosophisches Wörterbuch. Stuttgart. (venekeelne tõlge, 2003, Moskva. ISBN 5250017940.)
- ↑ Kaasik, Ülo, 2003. Matemaatikaleksikon. Tartu. ISBN 9985941772
- ↑ Weyl, Hermann, 1955. Symmetrie. Birkhäuser (zuerst Princeton, 1952.
- ↑ Tevet, J.-T., Tevet, E, 2015. Sümmeetria. S.E.R.R.,Tallinn. ISBN 9789949386949
| Tsitaadid Vikitsitaatides: Sümmeetria |